A classic interview question: “Please write a function fibonacci that takes an integer n and returns the nth Fibonacci number.” The Fibonacci sequence follows the following pattern:
0, 1, 1, 2, 3, 5, 8, 13…The pattern continues by adding the previous two Fibonacci numbers together and therefore, the next value above would be 21. Now let’s write a function to get the nth Fibonacci value so that,
// base Fibonacci numbers
fibonacci(0) // returns 0
fibonacci(1) // returns 1
// generated Fibonacci numbers
fibonacci(2) // returns 1
fibonacci(3) // returns 2
fibonacci(4) // returns 3
fibonacci(5) // returns 5
fibonacci(6) // returns 8
// ...Solution 1: Recursion
This is the most popular way of solving this problem because it is easier to reason about since,
fibonacci(n) = fibonacci(n - 1) + fibonacci(n - 2)Let’s write this as a function:
function fibonacci(n) {
return fibonacci(n - 1) + fibonacci(n - 2)
}This is great but, this has no stopping condition so it will go on forever. We need to specify that if n is 0 or 1 (our base Fibonacci numbers) we return 0 and 1 , respectively.
function fibonacci(n) {
if (n === 0) return 0
else if (n === 1) return 1
else return fibonacci(n - 1) + fibonacci(n - 2)
}Great! Try the function out for n = 1, n = 5, and n = 50.
fibonacci(1)should return1.fibonacci(5)should return5.fibonacci(50)should return12586269025.
You might have noticed that fibonacci(50) hangs in the console for some time. In fact, it took my console around eight minutes to execute!
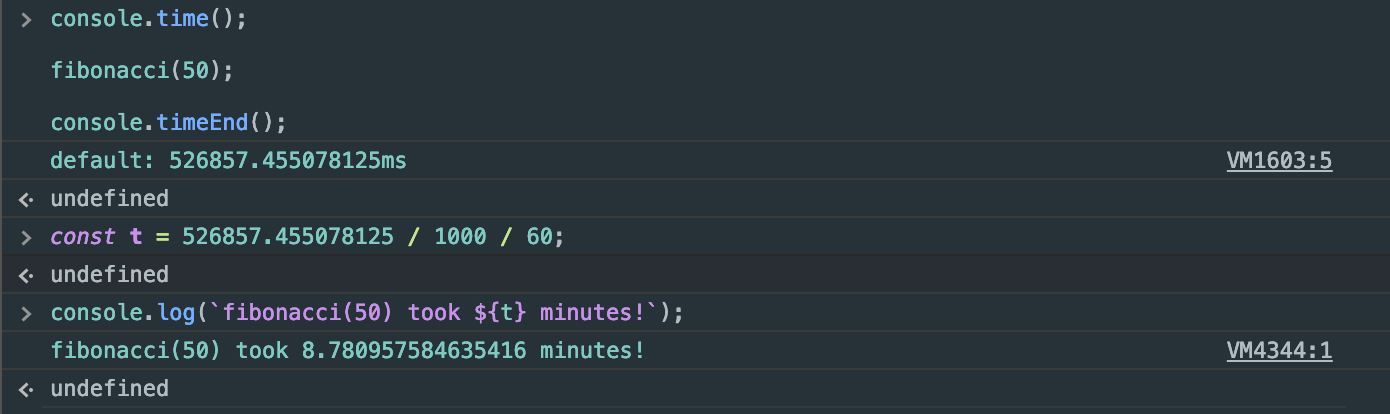
console showing an 8 minute execution of f(50)
This is the downside to this solution. For large n , the computation time takes way too long. The second solution fixes this problem.
Solution 2: Using a Generator Function
So the previous solution worked but, is super slow for large values of n.
Why is this the case? Well, let’s calculate fibonacci(10) as an example by hand (I will denote fibonacci as f for sake of simplicity.)
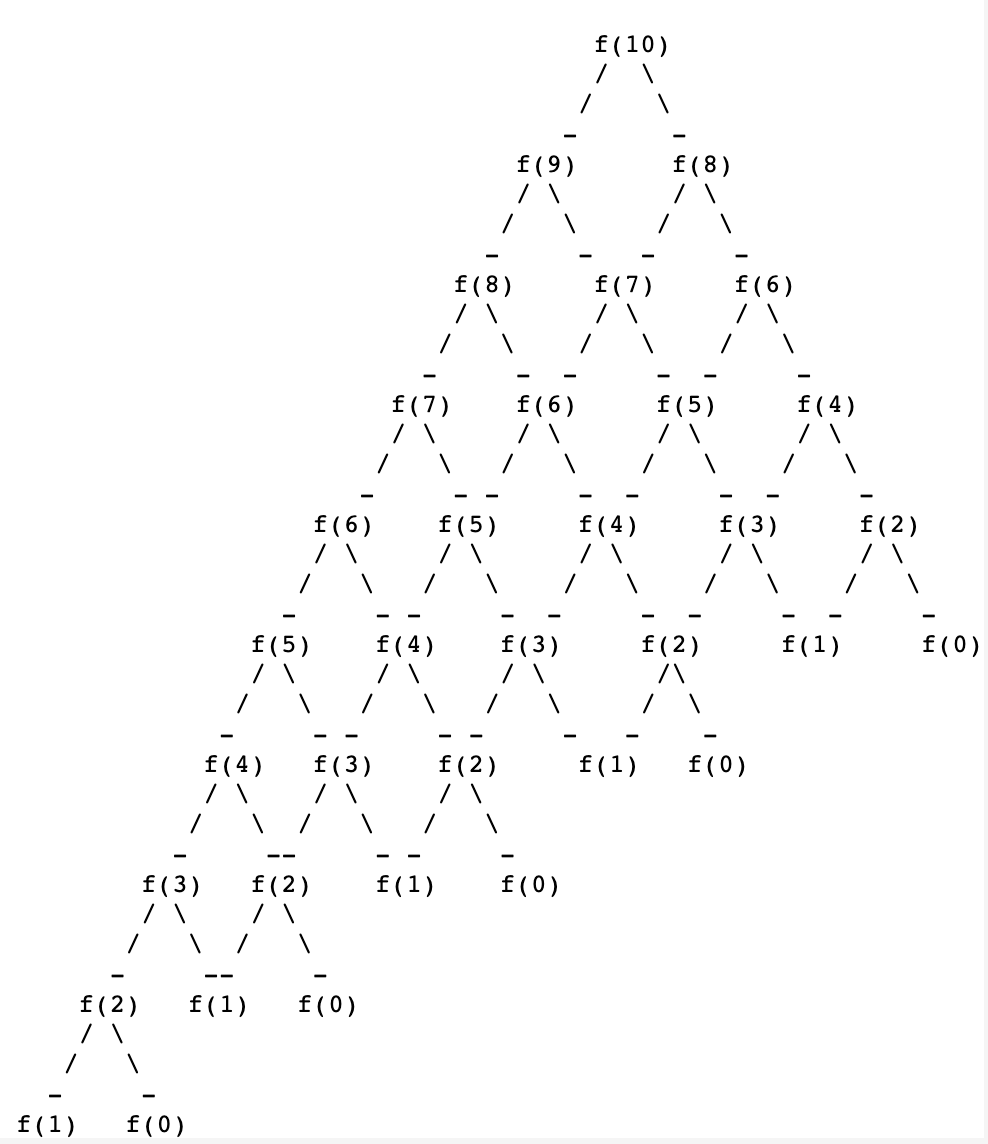
long recursive tree for f(10)
We are having to dive into a bunch of the same rabbit holes over and over again to calculate fibonacci(10). Why do we have to do this if all we need is the previous two Fibonacci numbers? Is there a way we can just remember the previous two Fibonacci numbers and generate the next Fibonacci number in the sequence? Yes! We can use generators to create an infinite sequence of Fibonacci numbers. Generators are interesting. They are like regular functions but with super powers. They are able to return values without completely ending the execution of a function. It does this by making use of the special yield statement. Let’s look at a trivial example of a generator function.
function* x() {
// the "*" denotes that function x is a generator
yield 'One taught me love'
yield 'One taught me patience'
yield 'And one taught me pain'
}Great! Let’s invoke this function to see how it works:
const thanku = x() // we invoke the generator
// invoke the `next` method on the generator prototype
thanku.next() // returns {value: "One taught me love", done: false}
thanku.next() // {value: "One taught me patience", done: false}
thanku.next() // {value: "And one taught me pain", done: false}
thanku.next() // {value: undefined, done: true}
// Now aren't you grateful for your x?For every call to the next method on the generator prototype, we get an object with two properties: value and done which is the value you are yielding from the generator and whether or not your generator is done generating values, respectively. Let’s look at a more interesting example. Let’s generate an infinite sequence of even numbers:
function* even() {
let start = 0
yield start // yield 0 as our first even number
while (true) {
// the start of our infinite sequence!
start += 2 // add 2 to start
yield start
}
}
function helper() {
const value = evenNumbers.next()
console.log(`NEXT: ${JSON.stringify(value)}`)
}
const evenNumbers = even()
setTimeout(helper, 1000)
setTimeout(helper, 2000)Let’s go though the execution of the code above together:
- We first Initialize the variable
evenNumberswith the invocation ofevengenerator. - We then wait
1000milliseconds for the first invocation ofhelper. -
1000milliseconds pass, andhelperis invoked- We initialize
valuewith the invocation ofevenNumbers.next - We initialize
startwith0 - Then we
yieldstartand pause the generator. - Now we
console.logthevalue
- We initialize
-
Wait another
1000milliseconds for the second invocation ofhelper- We enter the
whileloop - Increment
startby 2. yieldstartand pause the generator.- Now we
console.logthevalue.
- We enter the
Great! So how do we use the generator function to get the nth Fibonacci number? What we want to do is
- Create an infinite sequence of Fibonacci numbers using a generator.
- Keep invoking
Fibonacci.nextuntil we get the nth Fibonacci number.
1. Create an infinite sequence of Fibonacci numbers using a generator
function* Fibonacci() {
let a = 0,
b = 1 // base Fibonacci numbers
while (true) {
const c = a + b // next Fibonacci number
yield c
a = b // new a will be what used to be b
b = c // new b will be what used to be c
}
}2. Keep invoking Fibonacci.next until we have the nth number
We can do this by using a standard for loop:
function fibonacci(n) {
if (n === 0) return 0
else if (n === 1) return 1
else {
const Fib = Fibonacci()
let value
for (let i = 0; i < n - 1; i++) {
value = Fib.next().value
}
return value
}
}And there you have it: a faster function to find the nth Fibonacci number. Look at the difference in speed! ~8 minutes vs ~0.029 milliseconds!

console showing a 0.03 millisecond execution of f(50)
